Generating fake PNe positions from our images' surface
brightness - PNe8alpha
Rather than get into the conversions/systems/units/completeness/depth
questions of observed PNe data, we can apply the theoretical
relationship between light and PNe to generate 'artifical' PNe
positional data based on our distributions of light. Basically, we pick
values of alpha, the coefficient that relates luminosity to number of
PNe, and examine our images to generate, with some Monte Carlo action,
a possible distribution of PN. Here's how it works:
Start with the value of a pixel, convert that to Bolometric Luminosity
(with 0-point, distance, etc). Convert L_bol to N PNe by alpha (N =
alpha*L_bol). This will always turn out (with our images and our
selected values of alpha) to be a number between 0 and 1 - essentially
a probability. Select a random number between 0 and 1. If the value for
N is greater than the random number, we have a PN at this pixel.
Code Outline: clicking on the links will take you to that section of
the code - it's online, too, on a separate page.
Code --> PNe8alpha.sm -
PNe8alpha -
read fits image, set up running parameters/loops, call PNe8alphaw
PNe8alphaw - loop over all pixels, on each
pixel:
pick random number to compare with
calculated N, decide if it is a PN
convert PN coordinates from x,y
into RA/DEC, store in in file:
8.PNe.3.fits.alpha2523.RADEC.dat
write out .reg file of these
positions: 8.PNe.3.fits.alpha2523.reg [again, alpha25 means alpha_2.5
and alpha2523 means alpha_{2.5} = 23 x 10^-9
use command line ds9 to generate
jpg of overlaid coordinates (shown below)
Here are the results - our pretend PNe. These represent, for respective
values of alpha_{2.5}, the TOTAL number of PNe predicted to exist in
these images.
For all of these images we used a mask comprised of the
SExtracted/Monte Carloed object mask and the bright star hand mask. The
surface brightness mask (which we have normally been including at this
stage) was kept out of this process.
Our alpha_{2.5} values have been selected based on Feldmeier's
(?) citation of alpha_{2.5} to be 23 +10/-12 x 10^-9, and are 11, 23,
and 33 x 10^-9
Fields
alpha_{2.5} values
3
11 x 10^-9
23 x 10^-9
33 x 10^-9
4
11 x 10^-9
23 x 10^-9
33 x 10^-9
7
11 x 10^-9
23 x 10^-9
33 x 10^-9
Sub
11 x 10^-9
23 x 10^-9
33 x 10^-9
Core
11 x 10^-9
23 x 10^-9
33 x 10^-9
LPC
11
x 10^-9
23 x 10^-9
33 x 10^-9
FCJ
11
x 10^-9
23 x 10^-9
33 x 10^-9
3mm.fits
alpha_{2.5} = 11 x 10^-9

alpha_{2.5} = 23 x
10^-9

alpha_{2.5} = 33 x
10^-9

4mm.fits
alpha_{2.5} = 11 x 10^-9
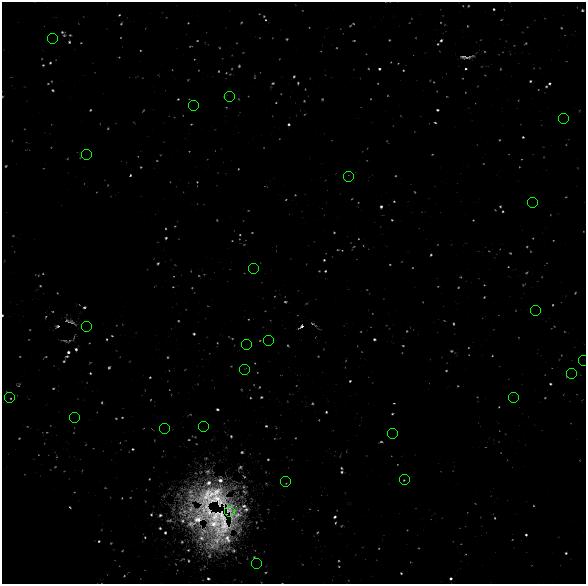
alpha_{2.5} = 23 x
10^-9

alpha_{2.5} = 33 x
10^-9

7mm.fits
alpha_{2.5} = 11 x 10^-9
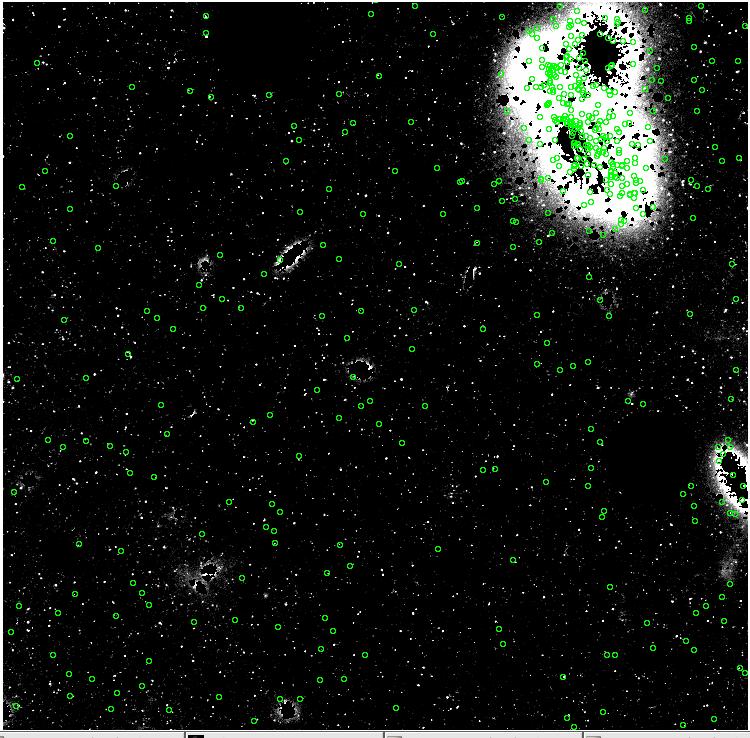
alpha_{2.5} = 23 x
10^-9
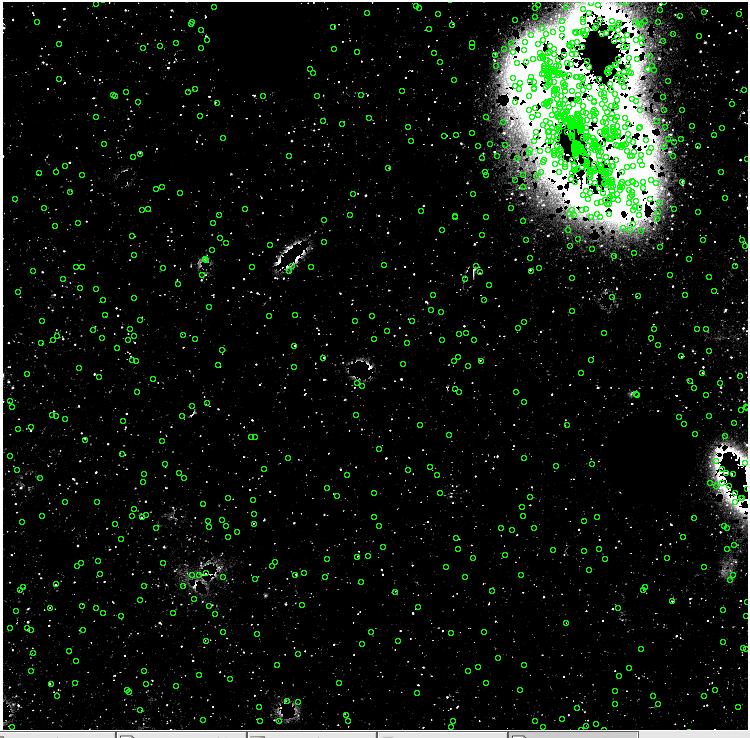
alpha_{2.5} = 33 x
10^-9
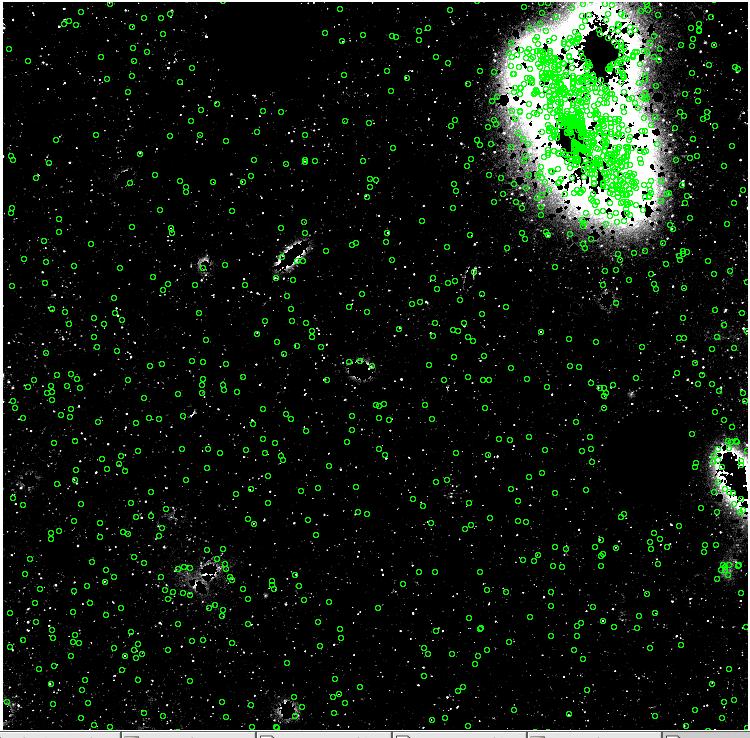
Submm.fits
alpha_{2.5} = 11 x 10^-9
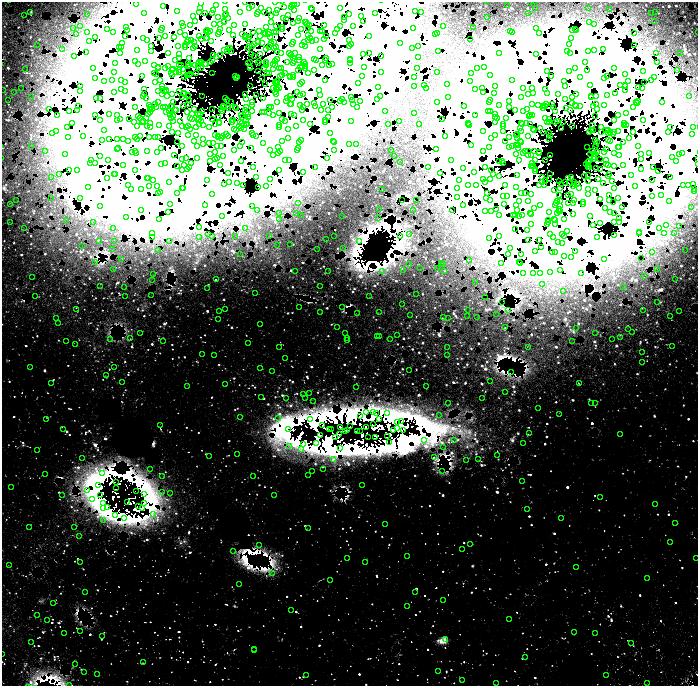
alpha_{2.5} = 23 x
10^-9

alpha_{2.5} = 33 x
10^-9
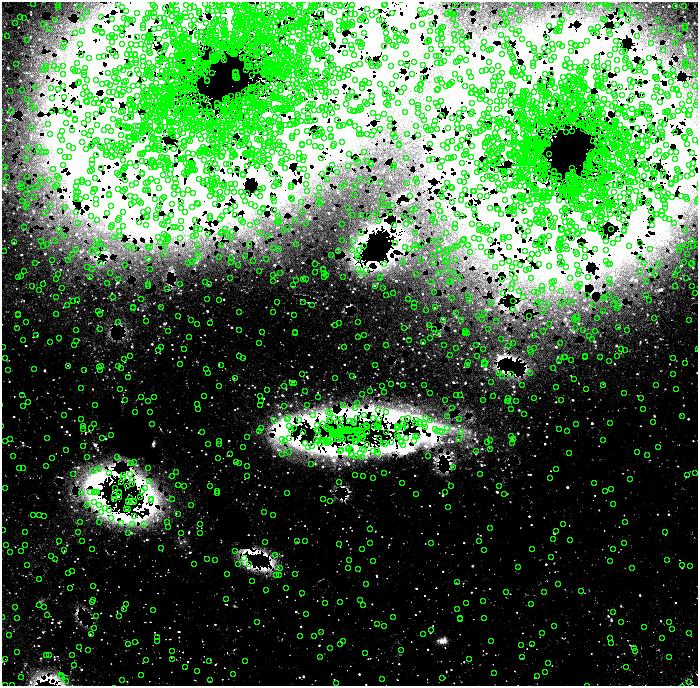
(isn't that pretty?........)
Coremm.fits
alpha_{2.5} = 11 x 10^-9
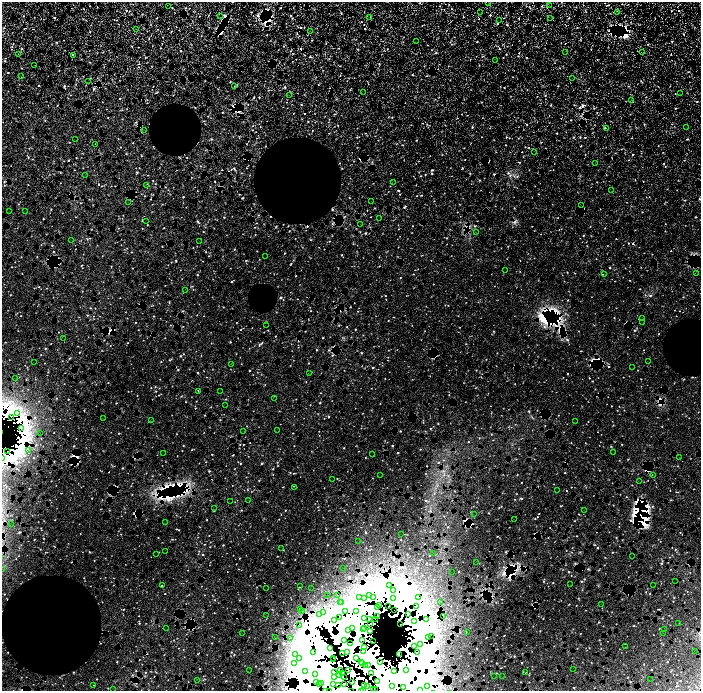
alpha_{2.5} = 23 x
10^-9
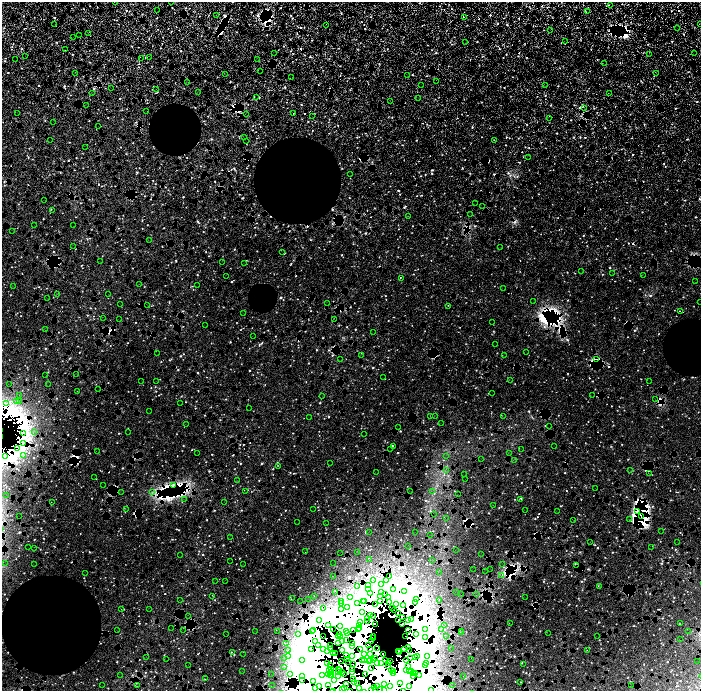
alpha_{2.5} = 33 x
10^-9
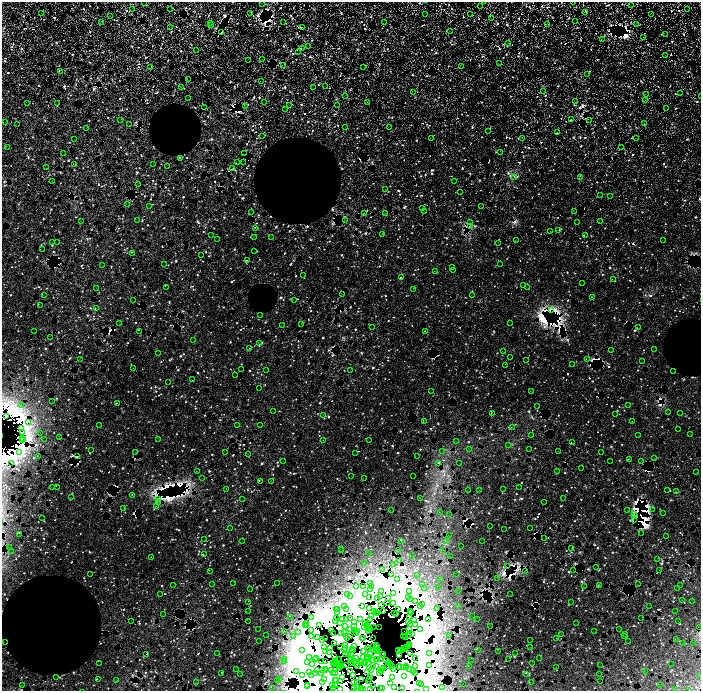
LPCmm.fits
alpha_{2.5} = 11 x 10^-9
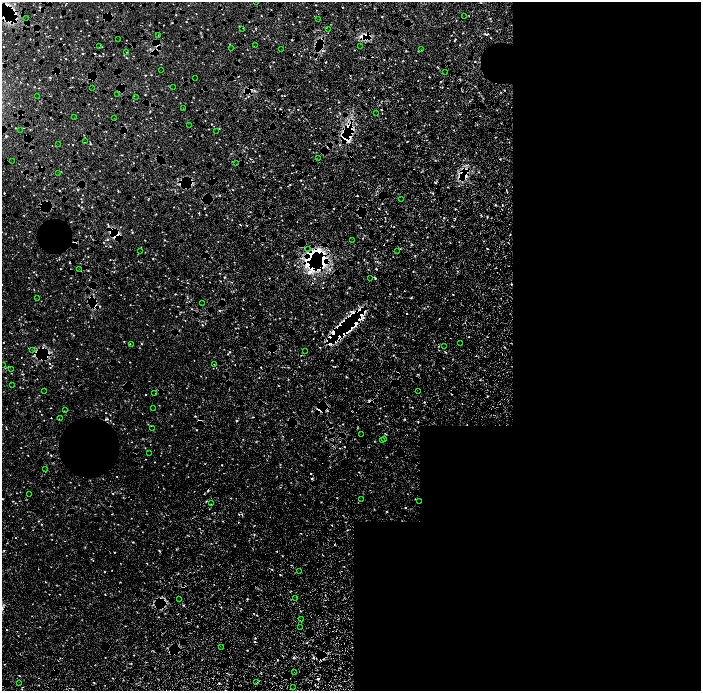
alpha_{2.5} = 23 x
10^-9
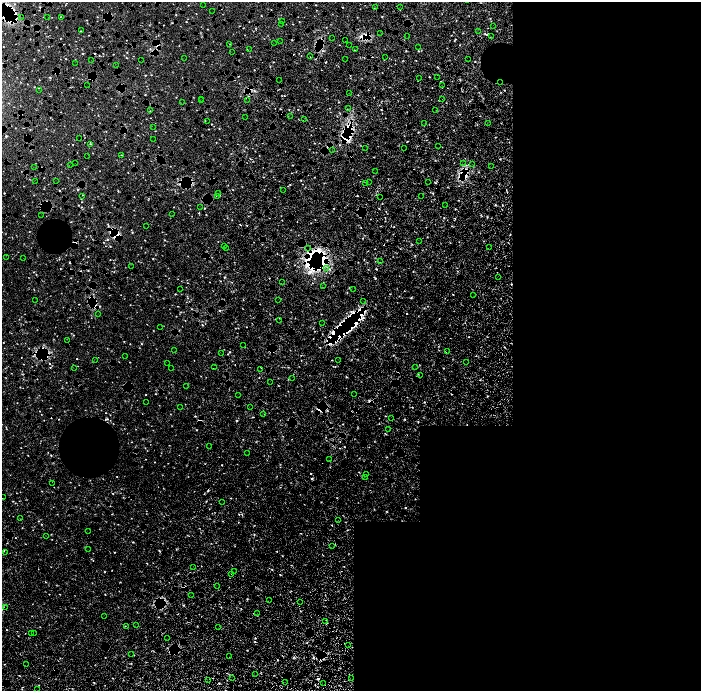
alpha_{2.5} = 33 x
10^-9
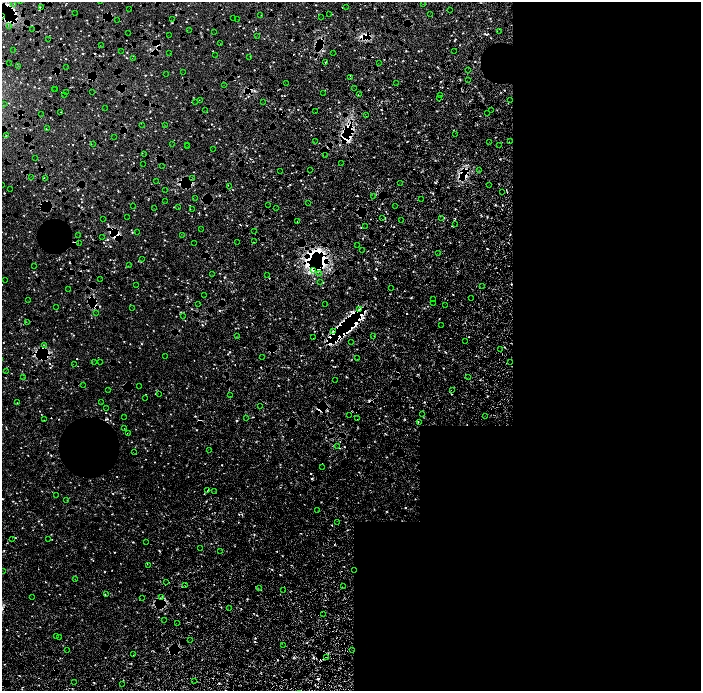
FCJmm.fits
alpha_{2.5} = 11 x 10^-9

alpha_{2.5} = 23 x
10^-9

alpha_{2.5} = 33 x
10^-9

back to main Virgo page




















