Astr 328 Homework #3: due 5pm, Friday April 18

IF you are sitting GREs, due in class April 21

---

1. The Radiation Era

• For a k=0 universe we showed that R~t^2/3 for a matter-dominated universe. In a radiation dominated universe, R(t) takes a different form. Derive the form of R(t) during the radiation era.

2. Volume of the Universe

• Show that in a q₀=1/2 universe,


• V(z) is different in different universes. For q₀=0 universe we have


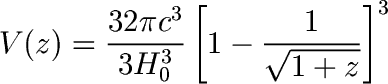
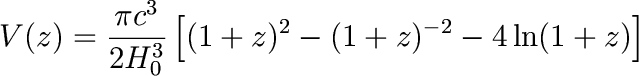
While for q₀=1 universe we have

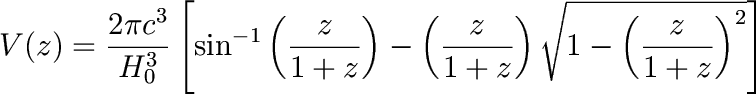
Plot V as a function of redshift for all three universes. (Note that while an q₀=0 universe is ruled out by other constraints, it is useful to study as the limiting case of a low density universe.)
• If the distribution of galaxies in the universe is completely homogeneous, now plot the (relative) number of galaxies you see as a function of redshift in each case.
• In the absence of magnitude selection effects (yeah, right!), if you could see all the galaxies in the universe out to a redshift of z=2, what would the median redshift of the galaxies be in these three universes?
• Why is this test (called the count-redshift test) a difficult test to perform?

3. Lookback Times and Age Constraints

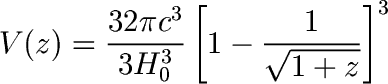
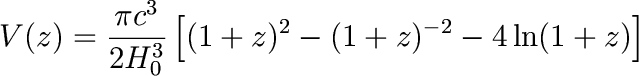
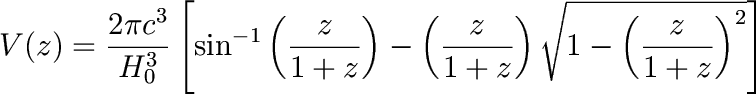
Use the "Cosmo" applet for this exercise.

• It's 1990. You are a good, party-line cosmologist and "know" that Omega=1, and that there is no such thing as the cosmological constant. You also "know" that globular clusters are 14-16 Gyr old. What can you say about H0?
• A few years later, you decide that the measurements of H0 are getting better, so you need to believe them. So take H0=55, and tell me what constraint you can place on Omega. What about if you believe H0=65? H0=75?
• And then Hipparcos comes along (around 1997) and tell us that GCs are further away, so the stars are more luminous than we thought, so they must be younger. The ages of the globular clusters get revised downwards to 11-13 Gyr. At the same time, you decide, for better or worse, that you like H0=65. Now what constraints can you place on Omega?
• Later, in 1998 the high redshift galaxy LBD53W091 was discovered. It lives at a redshift of z=1.55, and its was determined to have a minimum age of 3.5 Gyr. How does this change your constraints on Omega?
• Six months later, the age of LBD53W091 was revised downwards, and became 1.7 +/- 0.3 Gyr. NOW how do your constraints on Omega change?
• Finally, this wacky Lambda idea starts to take off, so you have to consider OmegaL as well. Given your GC ages and H0, pick values of OmegaL and, for those values, place limits on OmegaM. Make a plot of your results on an OmegaL-OmegaM plane, showing regions of "allowed cosmology" given your GC age constraints.

4. Group problem: What WMAP gave us